Strengthening password hashes by brute-forcing random data
Password hashes should be slow to prevent offline brute-force attacks. One way to make them slow is to include some unstored random data in the hash, which has to be brute-forced whenever a password is verified against a hash.
Adding entropy to the password
An attacker with access to the password hashes can do a brute-force attack on them, by guessing each password from a dictionary. To prevent this, verification of passwords should be relatively slow. This is typically done by a using a slow hash function, but an alternative is to make the password a little bit longer by adding some random data to it. This means that if we want to verify whether the password is correct, we have to brute-force that random data. This will significantly slow down verification of the password, which was our goal.
This method is called “password strengthening”, and the random data that is added to the password is called a “pepper”. Both are unfortunate names because these terms are sometimes also used for other mechanisms.
Password strengthening works by hashing a bit more than just the password. When a user chooses a password, the system will append some random data to the password. For example, we can pick a number between one and six. The password and the random number are concatenated and hashed, and that hash is stored. The random number is discarded.
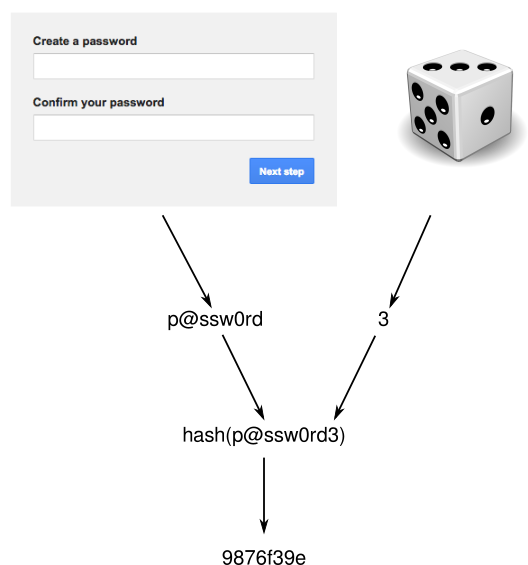
When the user then wants to authenticate and enters his password, we want to check it against the hash. We need the random number for this. However, we threw this number away in the previous step. The only way to check the hash is to brute-force the number. First we hash “p@ssw0rd1”, “p@ssw0rd2”, until we get the correct hash at “p@ssw0rd3”. If the user enters an incorrect password, we try all possible values one through six until we decline access.
Cost asymmetry
If an attacker gains access to the database and wants to crack the passwords, he would also have to crack the random data. By adding a random number between one and six, the attacker has to perform six times as much work to crack a password.
When trying the correct password, we have to try three times on average before we get the correct hash. In contrast, we have to try all six possible values before declining an incorrect password. An attacker has to try many incorrect passwords before finding the correct one. A normal user, however, will enter the correct password most of the time. Declining an incorrect password is thus twice as expensive as accepting a correct one. This is a disadvantage to the attacker.
Attacker trade-off
Even though the attacker has to do twice as much work on average, this method allows for a trade-off the attacker can make. For example, he can try to crack all the passwords with the secret data always set to 1. This will only work correctly in one sixth of the password hashes, but it will also take only one sixth of the time. The attacker has more options with this system on how much work to put in to cracking the passwords.
Collision resistance
Because the system now does a brute-force search for the correct hash, this increases the chance for hash collisions. A hash collision is when two passwords result in the same hash value. For example, both “secret” and “password” may result in the hash “fc9ec9ae”. Because only the hash is stored in the database, the system can no longer distinguish between these two passwords. Any one of them can be used to log in.
Normally, the hash for two passwords has to be exactly the same to result in a collision. In our example, however, we try six hashes instead of one. This increases the chance on hash collisions by six.
Fortunately, the chance for hash collisions is very small with modern hash functions. Even trying thousands of hashes will have a negligable increased risk of hash collisions.
Secret number of iterations
If we use an iterative hash function, we can also store our extra entropy in the number of iterations instead of in the password. Boyen suggests a specifically interesting mechanism in where the number of iterations is unbound and determined by the user. Imagine that when verifying a password, you never really know whether you have the incorrect password or that it was hashed with an iteration count you haven’t tried yet.
Conclusion
Adding random unstored data to passwords is an interesting way to slow down cracking password hashes. Unfortunately it has not really been researched enough to be safe to use in practice. Keep using bcrypt and scrypt.
Read more
- Authentication using random challenges, patent US5872917, Hellman, 1995
- A Simple Scheme to Make Passwords Based on One-Way Functions Much Harder to Crack, Udi Manber, 1996
- Strengthening Passwords, Abadi, 1997
- Method and apparatus for strengthening passwords for protection of computer systems, patent US6079021, Abadi, 1997
- Secure Applications of Low-Entropy Keys, Kelsey, 1997
- Brute Force Attack on UNIX Passwords with SIMD Computer, 1999
- Password-protection module, patent US7886345, Kaliski, 2004
- Halting Password Puzzles, Boyen, 2007
- CASH: A Cost Asymmetric Secure Hash Algorithm for Optimal Password Protection, Blocki, 2016





